“Computers are physical systems, and so are our brains. Therefore, they are subject to physical laws that determine what they can and cannot calculate,” points out Prof. Itai Arad, a theoretical physicist who researches the field of quantum information. He is determined to better understand physical systems by drawing on tools and insights from a variety of disciplines – including condensed matter physics, information theory, computer science and statistical mechanics.
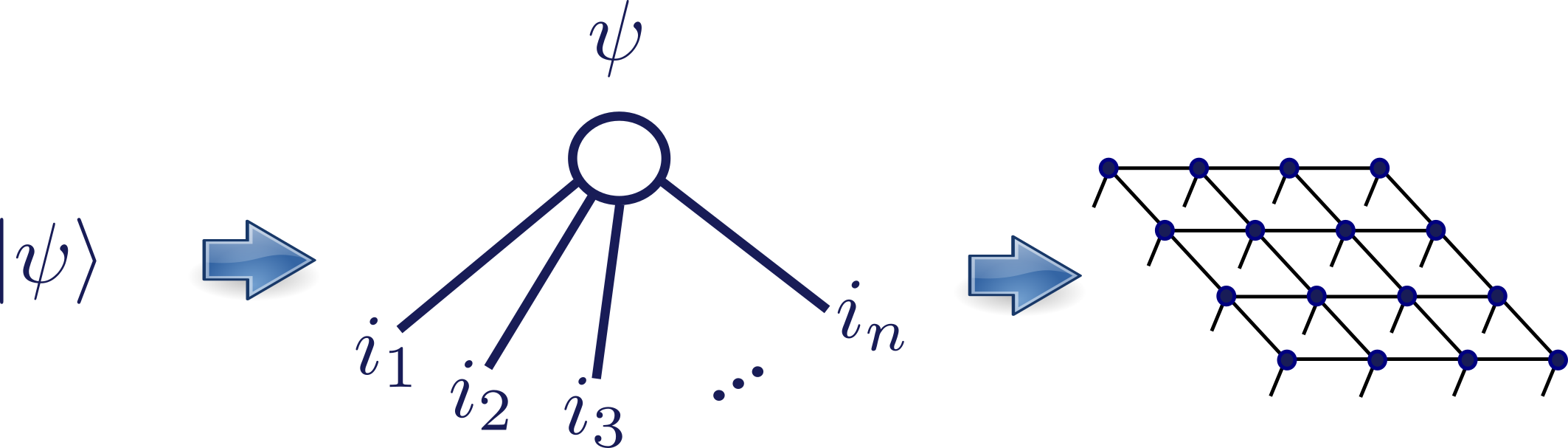
Specifically, Prof. Arad is intrigued by the fact that quantum systems require an enormous number of degrees of freedom to describe them. In the classical world, a system can be described by six “degrees of freedom” per particle – three position parameters and three velocity parameters – so that the number of degrees of freedom scales linearly with the system size. However, in the quantum world, where the concept of superposition exists, the number of degrees of freedom scales exponentially with the system size. For example, the state of a single spin can be described by two numbers but a system of 3 spins needs 8 parameters in order to be described (23). As the number of spins increases, the exponential number of parameters quickly becomes too large to manage. For just 100 spins, which is not a large amount, the number of degrees of freedom is already massive and too big even for the largest supercomputers.
An exponential amount of parameters is not necessarily a bad thing; as legendary physicist Richard Feynman noticed, if systems are exponentially hard to simulate using ordinary computers, then maybe they can be used as powerful computation devices. This way, by turning lemons into lemonade, the idea of quantum computers was born.
However, one might still ask whether this exponentiality is actually needed for the naturally occurring physical systems around us. “Do all natural quantum systems need so many parameters in order to be described faithfully? Are there quantum systems that can actually be well described by a number of degrees of freedom that scales linearly with the system size?” Prof. Arad’s research explores these key questions.
In fact, it turns out that the number of required parameters is intimately related to the extent of entanglement between the various particles in the system. Entanglement is a quantum phenomenon where particles interact in such a way that the quantum state of each particle cannot be described independently of the state of the others. According to Prof. Arad, when there is no entanglement, a linear number of parameters is sufficient, whereas in a highly entangled system, the number of required parameters is exponential to the system size.
This is a powerful way to understand the physical world, since it makes it possible to understand the physical properties of systems such as entanglement and low-temperature physics in terms of notions from information theory and computer science, including the amount of memory needed to represent such states. This is particularly useful for understanding local Hamiltonian systems such as magnets, ferromagnets and antiferromagnets.
Prof. Arad also examines to what extent the area law of entanglement entropy applies to different systems. “Entropy usually grows proportionally to the volume, not to the surface, but the fact that it grows proportionally to the surface in quantum systems is very interesting and is connected to the low level of entanglement and possibly to the fact that they can be represented by fewer degrees of freedom. We see this in black holes, for example.”
Although his work is theoretical, Prof. Arad is able to test his research on quantum computers such as the IBM quantum computer, which is accessible through the cloud.